

For example, the 2D Stokes Theorem immediately reduces to Green's Theorem. Course Outline with OLD (i.e wrong) midterm datesĪDDED April 12: Partial Solutions to Written Assignment 2.OFFICE HOURS FOR SANCHO: Wednesday and Friday 12:30 - 1:30 pm or by appointmentĬheck out how PDE's are being used to fight crime in LA! OFFICE HOURS FOR CHOKSI: Wednesday and Friday 1:30 - 2:30 PM or by appointment.
Grades will be posted on Minerva in the next few days.Ĭhoksi: April 29, 30, May 1 - 10:30 AM - 12 PM The My Courses site will be used ONLY for student discussions.ĪPRIL 23: Exams have been graded. We find that x = 0 or x = 1, our endpoints.MATH 264 - Advanced Calculus for Engineers MATH 264 - Advanced Calculus for Engineers - Winter 2013Īll important information about the course will be posted here. However, in this case, we also need to know the end points. Therefore, if we solve this, we find that r = 1.Īnytime we are looking for the area under a curve, we are looking for an indefinite integral. The displacement of a particle can be found by evaluating the integral between the two times given. The acceleration of the ball at this point is the double derivative of this equation.ĥ. The ball reaches its highest point at t = 4/10 seconds. To find this, take the derivative at set it to 0. To find the moment the ball reaches it highest point, we are looking for the moment the velocity is zero. Since we could look at the initial equation and see that it is an upward facing parabola, we could answer this part without actually taking the derivative but rather by knowing that a parabola’s concavity is always either upward and downward (depending on which way the parabola faces.)Ĥ. To determine concavity, let’s take the second derivative To find where a function increases or decreases, we need to take the derivativeĪt x = 4, this evaluates to 26, so this function is increasing at that point. Take the derivative of the top and bottom, and then evaluate the integral.ģ. Our best approach would be to use L’Hopital’s Rule. If the expression had evaluated to a real number, the problem would be done. If we plug in x=0 into the equation, we get a 0 in the denominator. Find the area enclosed by the graphs ofĢ. What is the total displacement between 0 seconds and 4 seconds?ħ. A particle moves in a straight line with the velocity given by the equation The height of the ball in meters at any given time can be found by the functionĪ) At what moment has the ball reached its highest point?ī) What is the acceleration of the ball at this point?ĥ. When x = 4, is the function increasing or decreasing? Is the function concave up, or concave down?Ĥ. A calculator is not needed for any of these problems.
#Advanced calculus practice problems free#
You need to be familiar with these concepts for the multiple choice and free response sections of the exam. Practice Calculus Problemsīelow is a smattering of different types of problems from across the AP Calculus AB curriculum.
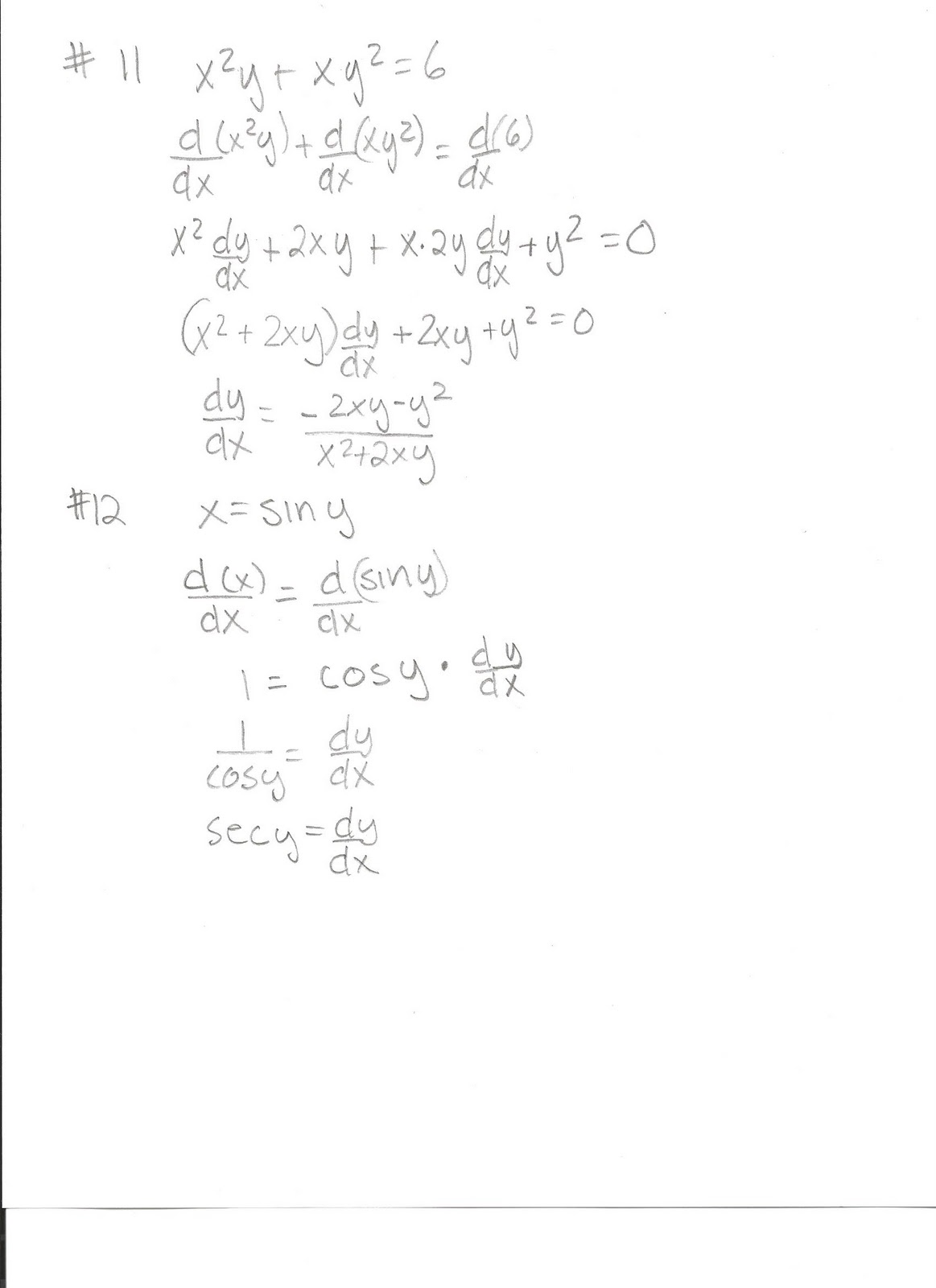
The College Board provides a few older exams, and you can buy College Board books that have others as well. The absolute best sources for problems is actual past AP exams. And learning the subject in theory, without ever working through examples, is rarely enough to truly understand how concepts can be implemented. It helps you gain confidence since many similar problems repeat themselves year after year (not the same problem, but similar types of problems). Going through practice problems will remind you of the possible topics that could be on the exam. It is important no matter what stage in AP Calculus preparation you are at. There is no such thing as doing too many practice calculus problems when studying for the AP exam.


 0 kommentar(er)
0 kommentar(er)
